
드디어 DFS, BFS를 공부할 시간이 왔다.
예전에 파이썬으로 코테 준비할때 찍먹한 적 있는데, 이번에 제대로 배워보려고한다.
(사실 조합 & 순열 공부할 차례인데 DFS로 해야 제일 쉽게 풀 수 있단다,, 백트래킹에서도 써먹고)
DFS&BFS는 그래프 탐색 알고리즘이라고도 한다.
대표적인 문제 유형
- 경로탐색 유형 (최단거리, 시간)
- 네트워크 유형 (연결)
- 조합 유형 (모든 조합 만들기)
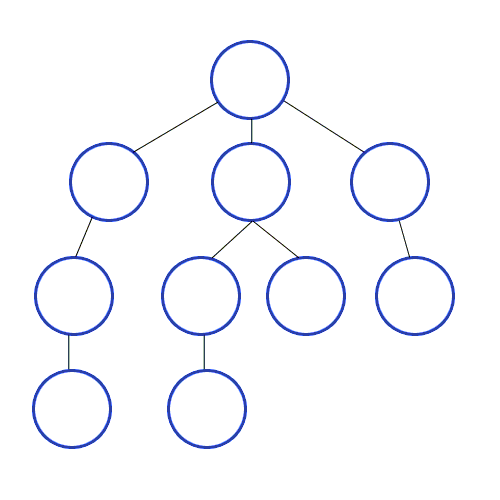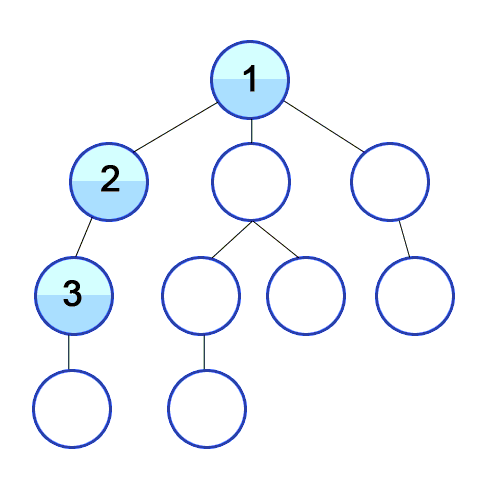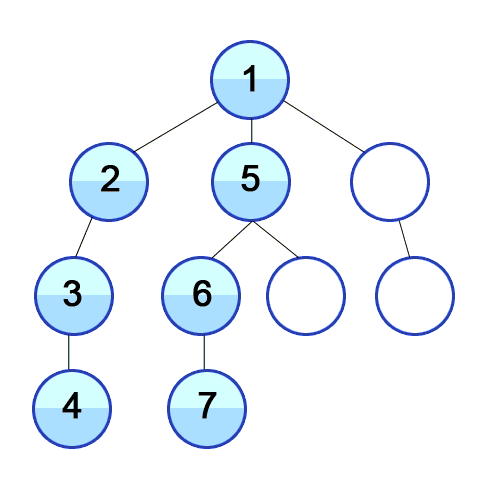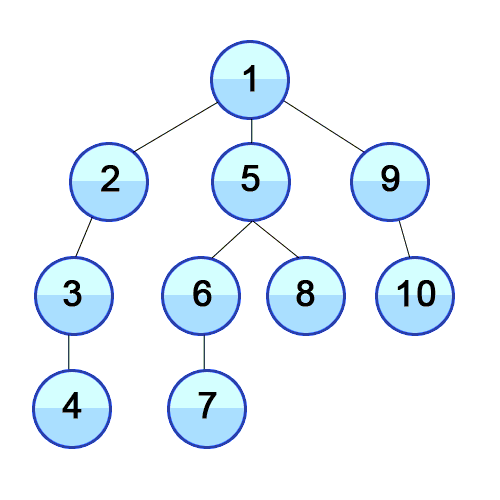
DFS - 깊이 우선 탐색
DFS는 루트 노드(or 일반 노드) 에서 다음 branch로 넘어가기 전에 해당 branch를 완벽하게 탐색하는 방식이다.
주로, 재귀함수나 Stack으로 많이 구현한다고 한다.
ex) 미로찾기에서 길을 찾다가 길이 막히면 마지막 갈래길로 돌아가는 방식
BFS - 너비 우선 탐색
BFS는 DFS와 다르게 자식 노드에서 모든 branch를 탐색하는게 아닌, 자식 노드를 모두 탐색해서 나아가는 방식이다.
주로 큐 / LinkedList로 많이 구현한다.
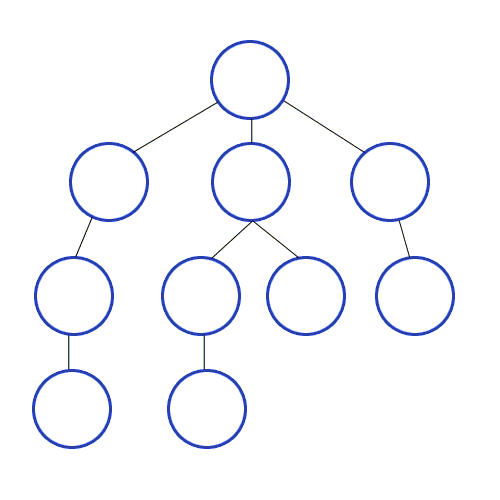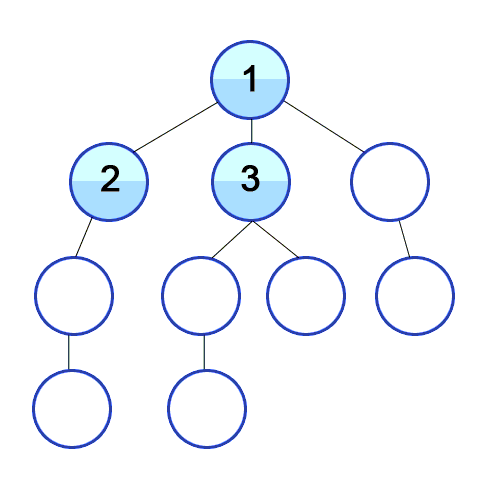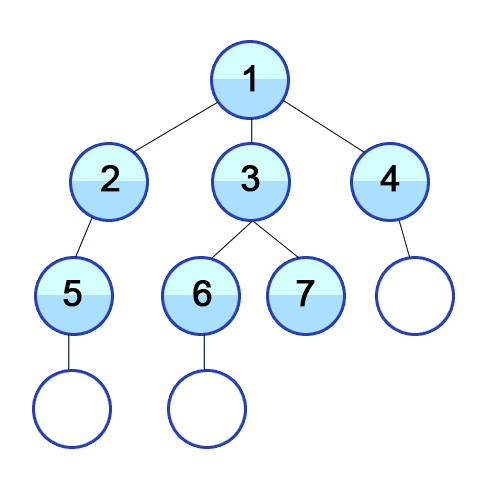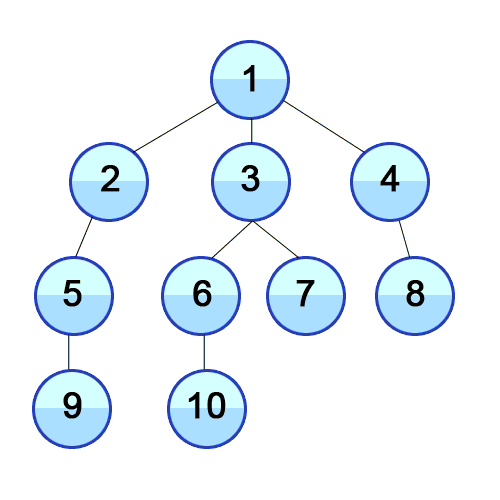
DFS vs BFS
둘 다 탐색을 하는 알고리즘이기 때문에 어떤걸 써도 정답은 나온다.
자신 있고 손에 익는 알고리즘을 쓰는게 좋은데 둘 다 알면 좋겠지?
사람들이 DFS를 더 선호하는 이유는 검증하기 쉽기 때문이다.
DFS는 하나의 조합을 완성해서 정답과 비교하는 식으로 동작한다.
정답을 비교하는 시점에서 내가 생각한대로 조합이 잘 나왔는지 확인하기 빠르고 쉽다.
반면에 BFS는 한번에 여러 조합들을 노드 한칸씩 만들다보니 조합이 완성되어서 정답과 비교하는 시점에
언제 어떻게 이렇게 만들어졌는지, 어디서부터 틀린건지 분석하기 어렵다.
코테에서는 알고리즘을 짧은 시간 내에 검증할 수 있어야하는데 DFS는 재귀함수만 알고 있어도 코드를 작성하기 쉽고, 내 답이 맞았는지 틀렸는지 검증하기 쉽다.
But, DFS도 단점이 있다. 하나의 조합을 완성하는데 시간이 오래 걸리는 조합이라면, 시간초과가 날 수도 있다.
만약 그럴거 같을때는 애초에 BFS로 시작해라.
백준 1260번 DFS와 BFS
문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
예제 입력 1
4 5 1
1 2
1 3
1 4
2 4
3 4
예제 출력 1
1 2 4 3
1 2 3 4
예제 입력 2
5 5 3
5 4
5 2
1 2
3 4
3 1
예제 출력 2
3 1 2 5 4
3 1 4 2 5
정답코드
1. 변수설정 & 입력값 받기
변수들을 static으로 선언한 이유는 static으로 선언을 해놓지 않으면 함수에서 사용할때 계속 매개변수로 넘겨줘야 해서 함수가 너무 복잡해짐
import java.io.*;
import java.util.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static int[][] arr;
static boolean[] visited;
static int N, M;
static Queue<Integer> queue = new LinkedList<>();
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
}
}
2. 함수 실행하기
- 배열에 N+1을 해준 이유는 노드의 번호를 배열의 인덱스와 맞춰주기 위함!
- 문제에서 간선은 양방향이라 했으니 arr[a][b]=1, arr[b][a]=1로 둘 다 맞춰줌
- dfs와 bfs에 시작노드(V)를 매개변수로 주고, 결과값을 static으로 선언한 StringBuilder에 넣어줌
- dfs종료 뒤에 visited 초기화 (bfs에서 또 써먹어야함)
arr = new int[N+1][N+1];
visited = new boolean[N+1];
for(int i = 0 ; i < M ; i ++) {
StringTokenizer str = new StringTokenizer(br.readLine());
int a = Integer.parseInt(str.nextToken());
int b = Integer.parseInt(str.nextToken());
arr[b][a] = 1;
arr[a][b] = 1;
}
dfs(V);
sb.append('\n');
visited = new boolean[N+1];
bfs(V);
System.out.println(sb.toString());
3. DFS구현 (재귀)
- 가장 먼저 오는 노드를 sb에 append
- 노드에 방문했으니 visited를 true로
- for문으로 V와 인접한 노드가 방문되지 않았다면 dfs(i)로 재귀
//dfs재귀함수로 구현
static void dfs(int V){
sb.append(V+" ");
visited[V] = true;
for(int i = 0 ; i <= N ; i ++) {
if(arr[V][i] ==1 && !visited[i]){
dfs(i);
}
}
}
4. BFS구현 (Queue)
- 큐에 시작노드 add
- 노드에 방문했으니 visitied true
- 큐에 시작노드가 있으니 while실행
- 큐를 poll 해서 노드를 v에 저장, sb에 appned
- dfs와 비슷하게 인접 노드를 모두 큐에 add하고, visited true
- 큐에 노드가 차있으니 while문 반복
//bfs Queue로 구현
static void bfs(int V){
queue.add(V);
visited[V] = true;
while(!queue.isEmpty()){
int v = queue.poll();
sb.append(v+" ");
for (int i = 0; i <= N ; i++) {
if(arr[v][i] ==1 && !visited[i]){
queue.add(i);
visited[i] = true;
}
}
}
}
5. 전체코드
import java.io.*;
import java.util.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static int[][] arr;
static boolean[] visited;
static int N, M;
static Queue<Integer> queue = new LinkedList<>();
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
arr = new int[N+1][N+1];
visited = new boolean[N+1];
for(int i = 0 ; i < M ; i ++) {
StringTokenizer str = new StringTokenizer(br.readLine());
int a = Integer.parseInt(str.nextToken());
int b = Integer.parseInt(str.nextToken());
arr[b][a] = 1;
arr[a][b] = 1;
}
dfs(V);
sb.append('\n');
visited = new boolean[N+1];
bfs(V);
System.out.println(sb.toString());
}
//dfs재귀함수로 구현
static void dfs(int V){
sb.append(V+" ");
visited[V] = true;
for(int i = 0 ; i <= N ; i ++) {
if(arr[V][i] ==1 && !visited[i]){
dfs(i);
}
}
}
//bfs Queue로 구현
static void bfs(int V){
queue.add(V);
visited[V] = true;
while(!queue.isEmpty()){
int v = queue.poll();
sb.append(v+" ");
for (int i = 0; i <= N ; i++) {
if(arr[v][i] ==1 && !visited[i]){
queue.add(i);
visited[i] = true;
}
}
}
}
}
마무리
DFS와 BFS는 자주 등장하는 알고리즘이고, 다른 알고리즘에서도 많이 써먹는 놈이니까
문제 많이 풀어서 응용할 수 있도록 ㄱㄱ
'알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 이진탐색 Binary Search (0) | 2024.07.30 |
|---|---|
| [ 알고리즘 ] 그래프 (1) | 2024.07.26 |
| [ 알고리즘 ] 스택을 이용한 VPS 판단 (5) | 2024.07.22 |
| [ 알고리즘 ] 유클리드 호제법 (0) | 2024.07.21 |
| [ 알고리즘 ] 에라토스테네스의 체 (0) | 2024.07.18 |
